| AffineTransformTest 図形の変形 |
H.Kamifuji . |
- はじめに
ここでは表示する図形の移動や回転など様々な変形方法について、事例にて説明します。
現在(2021/08)では、JDK-16.0.2 にアップされています。一部、上位互換について、見直しを行っていきます。
現在(2021/11)では、JDK-17.0.1 にアップされています。一部、上位互換について、見直しを行っていきます。
現在(2023/04)では、JDK-20.0.1 にアップされています。一部、上位互換について、見直しを行っていきます。
現在(2024/10)では、JDK-23 にアップされています。一部、上位互換について、見直しを行っていきます。
- 目 次
- Java2Dでの図形の変形方法とは
[ 目次 ]ここからは図形の変換について色々試してみます。
Java2Dで図形の移動や回転などを行うにはAffineTransformを使います。細かい説明は次のページから行いますので取り合えず簡単なサンプルを作ってみましょう。
Java2Dの座標系は左上が(0,0)の原点となっており、原点から右へ向かってX座標、原点から下に向かってY座標となっています。
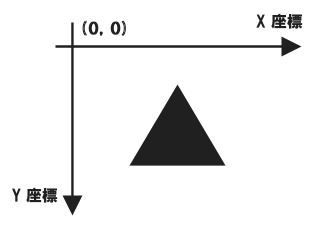
まず下記のようなコードで長方形を書いてみます。
下記のサンプルを実行してみよう。
/** * まず下記のようなコードで長方形を書いてみます。 */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest1_0 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest1_0 test = new AffineTransformTest1_0(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } }上記をコンパイルした後で実行すると次のように表示されます。

平行移動
では平行移動させてみましょう。まずAffinTransformオブジェクトを作成し、AffinTransformクラスのsetToTranslationメソッドを使って平行移動させてみます。
AffineTransform af = new AffineTransform(); af.setToTranslation(30d, 60d);
どのように移動するを決定したら、それをセットします。セットするにはGraphics2DクラスのsetTransformメソッドを使います。
g2.setTransform(af);
では先ほどのサンプルを少し修正してみましょう。
下記のサンプルを実行してみよう。
/** * Java2Dでの図形の変形方法とは 平行移動 */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest1_1 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest1_1 test = new AffineTransformTest1_1(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); af.setToTranslation(30d, 60d); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } }上記をコンパイルした後で実行すると次のように表示されます。
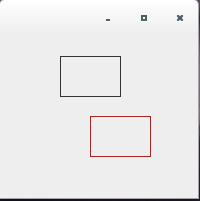
回転
次に回転を試してみます。AffinTransformオブジェクトに対して、AffinTransformクラスのrotatoメソッドを使ってどのくらい回転させるかを設定します。
AffineTransform af = new AffineTransform(); af.setToTranslation(30d, 60d); af.rotate(45 * Math.PI / 180); g2.setTransform(af);
上記の場合は、描画用座標に対してまず移動(setToTranslation)を行い、その後回転(rotato)をさせていることになります。
では先ほどのサンプルを少し修正してみましょう。
下記のサンプルを実行してみよう。
/** * 回転 */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest1_2 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest1_2 test = new AffineTransformTest1_2(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); af.setToTranslation(30d, 60d); af.rotate(45 * Math.PI / 180); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } }上記をコンパイルした後で実行すると次のように表示されます。
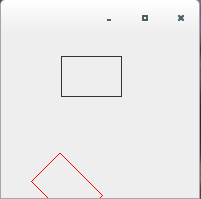
実のところ、移動させたあとで回転させているのではなく、移動と回転を別々に計算してその合成した結果が表示されています。何故こうなるのかは次のページから詳しく説明したいと思います。
- AffineTransformについて
[ 目次 ]ではAffineTransformについて見てみましょう。AffineTransformクラスは下記のように定義されています。
java.lang.Object ⇒ java.awt.geom.AffineTransform public class AffineTransform extends Object implements Cloneable, Serializable
コンストラクタは下記のようなものが用意されています。
コンストラクタ AffineTransform()
恒等変換を表現する新しい AffineTransform を構築します。AffineTransform(AffineTransform Tx)
指定された AffineTransform オブジェクトのコピーである、新しい AffineTransform を構築します。AffineTransform(double[] flatmatrix)
3×3 変換行列の 4 つの非平行移動エントリまたは 6 つの指定可能エントリのどちらかを表現する倍精度値の配列から、新しい AffineTransform を構築します。AffineTransform(double m00, double m10, double m01, double m11, double m02, double m12)
3×3 変換行列の 6 つの指定可能エントリを表現する 6 つの倍精度値から、新しい AffineTransform を構築します。AffineTransform(float[] flatmatrix)
3×3 変換行列の 4 つの非平行移動エントリまたは 6 つの指定可能エントリのどちらかを表現する浮動小数点値の配列から、新しい AffineTransform を構築します。AffineTransform(AffineTransform Tx)
指定された AffineTransform オブジェクトのコピーである、新しい AffineTransform を構築します。AffineTransform(float m00, float m10, float m01, float m11, float m02, float m12)
3×3 変換行列の 6 つの指定可能エントリを表現する 6 つの浮動小数点値から、新しい AffineTransform を構築します。
AffineTransformは二次元の座標を他の二次元の座標に変換するのに用いられます。簡単な使い方は前のページで見た通りですがAffineTransformを使った変換方法についてもう少し細かく見てみます。
AffineTransformによる変換について
では実際にAffineTransformを使ってどのように変換しているのかを見てみましょう。例えば頂点(x, y)をAffineTransformを使って変換する場合、下記のような3×3の配列による変換をしています。
[ x'] [ m00 m01 m02 ] [ x ] [ m00x + m01y + m02 ] [ y'] = [ m10 m11 m12 ] [ y ] = [ m10x + m11y + m12 ] [ 1 ] [ 0 0 1 ] [ 1 ] [ 1 ]
ここで元の座標(x, y)はAffineTransformを使って新しい座標(x', y')に変換されます。実際の値は、
x' = m00 * x + m01 * y + m02 y' = m10 * x + m11 * y + m12
となるわけです。
上記を見て頂くと分かる通り、m02とm12がX軸とY軸の平行移動する場合に関係する値です。
例えばX軸方向に4ピクセル移動させたいのであれば、物体の各頂点のX座標をそれぞれ"+ 4"すればいいので
[ 1 0 4 ] [ x ] [ x' ] [ 0 1 0 ] ~ [ y ] = [ y' ] [ 0 0 1 ] [ 1 ] [ w' ] x' = x + 4 y' = y
のような変換をすればいいことになります。
変換行列の値の取得
AffineTransformのgetMatrixメソッドを使って現在設定されている変換行列の値を取得することができます。
getMatrix public void getMatrix(double[] flatmatrix)
3×3 アフィン変換行列内の 6 つの指定可能な値を取り出し、倍精度値の配列に配置します。各値は配列に { m00, m10, m01, m11, m02, m12 }という形式で格納されます。
4 つの double 値の配列も指定できます。その場合は、配列の非平行移動部分を表す最初の 4 つの要素だけが取り出され、値は配列に { m00, m10, m01, m11 } という形式で格納されます。
パラメータ:
flatmatrix - 戻り値を格納するために使用する double 値の配列
ではデフォルトコンストラクタの場合の値を取り出してみましょう。
下記のサンプルを実行してみよう。
/** * AffineTransformについて デフォルトコンストラクタの場合の値を取り出し */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest2_1 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest2_1 test = new AffineTransformTest2_1(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); double[] flatmatrix = new double[6]; AffineTransform af = new AffineTransform(); af.getMatrix(flatmatrix); printMatrix(flatmatrix); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行すると下記のように出力されます。
[ 1.0 0.0 0.0 ] [ 0.0 1.0 0.0 ]
デフォルトでは単位行列になるようです。
では45度回転させた場合も見てみます。
下記のサンプルを実行してみよう。
/** * 45度回転させた場合 */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest2_2 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest2_2 test = new AffineTransformTest2_2(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); double[] flatmatrix = new double[6]; AffineTransform af = new AffineTransform(); af.rotate(45 * Math.PI / 180); af.getMatrix(flatmatrix); printMatrix(flatmatrix); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行すると下記のように出力されます。
[ 0.7071067811865476 -0.7071067811865475 0.0 ] [ 0.7071067811865475 0.7071067811865476 0.0 ]
デフォルト以外のコンストラクタ
では他のコンストラクタも確認してみましょう。
AffineTransform public AffineTransform(double m00, double m10, double m01, double m11, double m02, double m12)3×3 変換行列の 6 つの指定可能エントリを表現する 6 つの倍精度値から、新しい AffineTransform を構築します。
パラメータ:
m00, m01, m02, m10, m11, m12 - 3x3 変換行列を構成する 6 つの浮動小数点値
このコンストラクタを使用すると、
[ m00 m01 m02 ] [ m10 m11 m12 ] [ 0 0 1 ]
のように値が設定されます。これも試してみましょう。
下記のサンプルを実行してみよう。
/** * デフォルト以外のコンストラクタ */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest2_3 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest2_3 test = new AffineTransformTest2_3(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); double[] flatmatrix = new double[6]; AffineTransform af = new AffineTransform(0.1d, 0.2d, 0.3d, 0.4d, 0.5d, 0.6d); af.getMatrix(flatmatrix); printMatrix(flatmatrix); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }上記をコンパイルした後で実行すると次のように表示されます。
[ 0.1 0.3 0.5 ] [ 0.2 0.4 0.6 ]
今回の3事例では、下記のような枠のみのウインドウが表示されます。
- 平行移動について
[ 目次 ]先ほどのページでも少し書きましたが、例えばX軸方向に"+40"、Y軸方向に"+30"させたい場合には次のような変換行列を設定すればいいことになります。
[ 1 0 40 ] [ x ] [ x' ] [ 0 1 30 ] ~ [ y ] = [ y' ] [ 0 0 1 ] [ 1 ] [ w' ] x' = x + 40 y' = y + 30
このようにするにはコンストラクタで変換行列の値を渡してAffineTransformを作成するか、AffineTransformのsetTransformメソッドを使って変換行列を設定します。
setTransform public void setTransform(double m00, double m10, double m01, double m11, double m02, double m12)この変換を 6 つの倍精度値によって指定されている行列に設定します。
パラメータ:
m00, m01, m02, m10, m11, m12 - 3x3 変換行列を構成する 6 つの浮動小数点値
実際に簡単なサンプルを作成して試してみます。平行移動しつつ、変換行列の値を標準出力に出すようにします。
下記のサンプルを実行してみよう。
/** * 平行移動について */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest3_1 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest3_1 test = new AffineTransformTest3_1(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); af.setTransform(1.0d, 0.0d, 0.0d, 1.0d, 40.0d, 30.0d); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 1.0 0.0 40.0 ] [ 0.0 1.0 30.0 ]
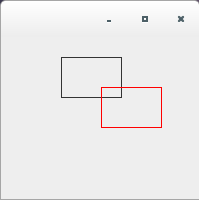
setToTranslationメソッド
平行移動の場合には先ほどのように変換行列を自分で設定してもいいのですが、setToTranslationというメソッドが用意されているのでそれを使っても結構です。
setToTranslation public void setToTranslation(double tx, double ty)この変換を平行移動変換に設定します。この変換を表現する行列は次のようになります。
[ 1 0 tx ]
[ 0 1 ty ]
[ 0 0 1 ]
パラメータ:
tx - 座標が X 軸方向で平行移動される距離
ty - 座標が Y 軸方向で平行移動される距離
これは平行移動に特化したAffineTransformを作成したい時に便利です。注意点としては、元の行列にどのような値が設定されていた場合でも、上記の行列に置き換えられてしまうという点です。
では、これも簡単なサンプルで試してみます。
下記のサンプルを実行してみよう。
/** * setToTranslationメソッド */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest3_2 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest3_2 test = new AffineTransformTest3_2(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); af.setToTranslation(40.0d, 30.0d); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 1.0 0.0 40.0 ] [ 0.0 1.0 30.0 ]
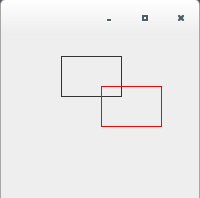
translateメソッド
平行移動には実はもう1つメソッドがあります。translateメソッドを使っても平行移動が行えます。
translate public void translate(double tx, double ty)この変換を平行移動変換に連結します。これは、concatenate(T) を呼び出すことに相当します。ただし、T は次の行列で表現される AffineTransform です。
[ 1 0 tx ]
[ 0 1 ty ]
[ 0 0 1 ]
パラメータ:
tx - 座標が X 軸方向で平行移動される距離
ty - 座標が Y 軸方向で平行移動される距離
先ほどのsetToTranslationの場合は変換行列を完全に置き換えていましたが、translateの場合は置き換えではなく、既存の変換行列に新たに乗算を行い、その結果を新しい変換行列の値とします。
例えば既存の変換行列が下記左のような行列だった場合、trasnlateメソッドを実行することで、右の行列のような新しい変換行列になります。
[ m00 m01 m02 ] [ 1 0 tx ] [ m00 m01 m00*tx + m01*ty + m02] [ m10 m11 m12 ] ~ [ 0 1 ty ] [ m10 m11 m10*tx + m11*ty + m12] [ m20 m21 m22 ] [ 0 0 1 ] [ m20 m21 m20*tx + m21*ty + m22]
translateメソッドでは行列の右側の値以外は影響を受けません。平行移動に関する右側の値だけ上記のような値に変換します。これも簡単なサンプルで試して見ましょう。
下記のサンプルを実行してみよう。
/** * translateメソッド */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest3_3 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest3_3 test = new AffineTransformTest3_3(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); af.setTransform(0.75d, 0.0d, 0.0d, 0.75d, 10.0d, 20.0d); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); System.out.println(); af.translate(40.0d, 30.0d); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 0.75 0.0 10.0 ] [ 0.0 0.75 20.0 ] [ 0.75 0.0 40.0 ] [ 0.0 0.75 42.5 ]
上が変換前の値で、下がtranslateした後の値です。ちなみに実行結果は下記のようになります。

今回の件とは関係ありませんが、単位行列の部分の値を変更することで、拡大や縮小ができます。
- 回転について
[ 目次 ]では次は回転についてです。回転の場合であっても自分で適切な値の変換行列を設定すればできるのですが、結構計算が面倒だと思いますので、用意されているメソッドを使います。平行移動の時と同様に回転に関しても2つのメソッドが用意されています。
まずsetToRotationメソッドから見てみます。
setToRotation public void setToRotation(double theta)
この変換を回転変換に設定します。この変換を表現する行列は次のようになります。
[ cos(theta) -sin(theta) 0 ] [ sin(theta) cos(theta) 0 ] [ 0 0 1 ]正の角度 theta で回転すると、正の x 軸の点が正の y 軸に向かって回転されます。
パラメータ:
theta - ラジアンで表した回転角度
ここで指定する角度の単位はラジアンです。角度の指定する時はjava.lang.Mathクラスで定義されているPIを使うと便利です。
java.lang.Math.PI = 180度 Math.PI / 2 = 90度 Math.PI / 3 = 60度 Math.PI / 4 = 45度 Math.PI / 6 = 30度
実際に簡単なサンプルを作成して試してみます。回転させ、その変換行列の値を標準出力に出すようにします。
下記のサンプルを実行してみよう。
/** * 回転について */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest4_1 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest4_1 test = new AffineTransformTest4_1(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); System.out.println(); af.setToRotation(30 * Math.PI/180); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 1.0 0.0 0.0 ] [ 0.0 1.0 0.0 ] [ 0.8660254037844387 -0.49999999999999994 0.0 ] [ 0.49999999999999994 0.8660254037844387 0.0 ]
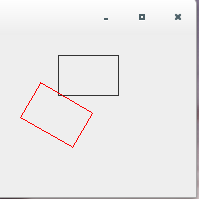
setToRotationの場合には、対象となる変換行列にどのような値が設定されていたとしても完全に新しい行列に置き換えてしまいます。
rotateメソッド
回転のもう1つのメソッドにrotateメソッドがあります。
rotate public void rotate(double theta)
この変換を回転変換に連結します。これは、concatenate(R) を呼び出すことに相当します。ただし、R は次の行列で表現される AffineTransform です。
[ cos(theta) -sin(theta) 0 ] [ sin(theta) cos(theta) 0 ] [ 0 0 1 ]正の角度 theta で回転すると、正の x 軸の点が正の y 軸に向かって回転されます。
パラメータ:
theta - ラジアンで表した回転角度
先ほどのsetToRotationの場合は変換行列を完全に置き換えていましたが、rotateの場合は置き換えではなく、既存の変換行列に新たに乗算を行い、その結果を新しい変換行列の値とします。
例えば既存の変換行列が下記左のような行列だった場合、rotateメソッドを実行することで、右の行列のような新しい変換行列になります。
[ m00 m01 m02 ] [ cos(t) -sin(t) 0 ] [ m10 m11 m12 ] × [ sin(t) cos(t) 0 ] [ m20 m21 m22 ] [ 0 0 1 ] [ m00 * cos(t) + m01*sin(t) m00 * (-sin(t)) + m01*cos(t) m02 ] = [ m10 * cos(t) + m11*sin(t) m10 * (-sin(t)) + m11*cos(t) m12 ] [ m20 * cos(t) + m21*sin(t) m20 * (-sin(t)) + m21*cos(t) m22 ]見ていただくと分かるとおり、rotateメソッドでは、実行前と後で変換行列の右側(平行移動に関する列)の列は影響を受けません。
では、これも簡単なサンプルで試してみます。
下記のサンプルを実行してみよう。
/** * rotateメソッド */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest4_2 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest4_2 test = new AffineTransformTest4_2(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); System.out.println(); af.setTransform(1.0d, 0.0d, 0.0d, 1.0d, 10.0d, 20.0d); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); System.out.println(); af.rotate(40 * Math.PI/180); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.blue); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 1.0 0.0 0.0 ] [ 0.0 1.0 0.0 ] [ 1.0 0.0 10.0 ] [ 0.0 1.0 20.0 ] [ 0.766044443118978 -0.6427876096865393 10.0 ] [ 0.6427876096865393 0.766044443118978 20.0 ]
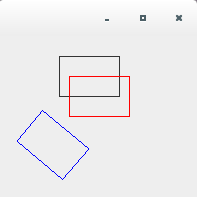
もう1つのsetToRotationメソッド
最初に見てみたsetToRotationメソッドには引数が違うもう1つのメソッドが用意されています。
setToRotation public void setToRotation(double theta, double x, double y)この変換を平行移動後の回転変換に設定します。このオペレーションは、座標をアンカーポイントが原点 (S1) になるように移動し、これらの座標を新しい原点 (S2) を中心に回転してから、最後にその仲介的な原点を元のアンカーポイント (S3) の座標に戻すために移動することに相当します。
この操作は、次の一連の呼び出しに相当します。
setToTranslation(x, y); // S3: final translation rotate(theta); // S2: rotate around anchor translate(-x, -y); // S1: translate anchor to originこの変換を表現する行列は次のようになります。
[ cos(theta) -sin(theta) x-x*cos+y*sin ] [ sin(theta) cos(theta) y-x*sin-y*cos ] [ 0 0 1 ]正の角度 theta で回転すると、正の x 軸の点が正の y 軸に向かって回転されます。
パラメータ:
theta - ラジアンで表した回転角度
x, y - 回転のアンカーポイントの座標
簡単に書いてしまうと、指定した点を中心として回転させたい場合などに使えます。
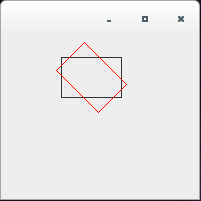
これも簡単なサンプルで試して見ましょう。最初の図形の真中を中心点として回転させてみます。
下記のサンプルを実行してみよう。
/** * もう1つのsetToRotationメソッド */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest4_3 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest4_3 test = new AffineTransformTest4_3(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); System.out.println(); af.setToRotation(45 * Math.PI/180, 90d, 40d); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 0.7071067811865476 -0.7071067811865475 54.644660940672615 ] [ 0.7071067811865475 0.7071067811865476 -51.923881554251174 ]
- 拡大縮小について
[ 目次 ]では次に拡大と縮小です。例えばX軸方向に"2倍"、Y軸方向に"1/2倍"させたい場合には次のような変換行列を設定すればいいことになります。
[ 2 0 0 ] [ x ] [ x' ] [ 0 0.5 0 ] × [ y ] = [ y' ] [ 0 0 1 ] [ 1 ] [ w' ] x' = 2x y' = 0.5y
拡大縮小の場合は簡単ですので自分で設定しても問題ないかと思います。ただメソッドを使った方が簡単は簡単なので拡大縮小についても2つのメソッドを確認してみます。
setToScale
まずsetToScaleメソッドから見てみます。
setToScale public void setToScale(double sx, double sy)この変換をスケーリング変換に設定します。この変換を表現する行列は次のようになります。
[ sx 0 0 ] [ 0 sy 0 ] [ 0 0 1 ]パラメータ:
sx - 座標を X 軸方向にスケーリングするために使う係数
sy - 座標を Y 軸方向にスケーリングするために使う係数
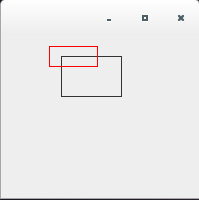
実際に簡単なサンプルを作成して試してみます。縮小させ、その変換行列の値を標準出力に出すようにします。
下記のサンプルを実行してみよう。
/** * 拡大縮小について */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest5_1 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest5_1 test = new AffineTransformTest5_1(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); System.out.println(); af.setToScale(0.8d, 0.5d); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 1.0 0.0 0.0 ] [ 0.0 1.0 0.0 ] [ 0.8 0.0 0.0 ] [ 0.0 0.5 0.0 ]
setToScaleの場合には、対象となる変換行列にどのような値が設定されていたとしても完全に新しい行列に置き換えてしまいます。
scaleメソッド
次にscaleメソッドについてです。
scale public void scale(double sx, double sy)この変換をスケーリング変換に連結します。これは、concatenate(S) を呼び出すことに相当します。ただし、S は次の行列で表現される AffineTransform です。
[ sx 0 0 ] [ 0 sy 0 ] [ 0 0 1 ]パラメータ:
sx - 座標を X 軸方向にスケーリングするために使う係数
sy - 座標を Y 軸方向にスケーリングするために使う係数
先ほどのsetToScaleの場合は変換行列を完全に置き換えていましたが、scaleの場合は置き換えではなく、既存の変換行列に新たに乗算を行い、その結果を新しい変換行列の値とします。
例えば既存の変換行列が下記左のような行列だった場合、scaleメソッドを実行することで、右の行列のような新しい変換行列になります。
[ m00 m01 m02 ] [ sx 0 0 ] [ m00*sx m01*sy m02] [ m10 m11 m12 ] × [ 0 sy 0 ] = [ m10*sx m11*sy m12] [ m20 m21 m22 ] [ 0 0 1 ] [ m20*sx m21*sy m22]
scaleメソッドでは、実行前と後で変換行列の右側の列は影響を受けません。その為、平行移動に関する値が設定されていた場合にscaleメソッドを実行してもその部分は変化がありません。
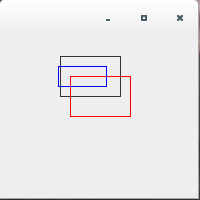
では、これも簡単なサンプルで試してみます。
下記のサンプルを実行してみよう。
/** * scaleメソッド */ import java.awt.*; import java.awt.geom.*; import java.awt.event.*; import javax.swing.*; public class AffineTransformTest5_2 extends JPanel{ public static void main(String[] args){ JFrame frame = new JFrame(); AffineTransformTest5_2 test = new AffineTransformTest5_2(); frame.getContentPane().add(test); frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); frame.setBounds( 0, 0, 200, 200); frame.setVisible(true); } public void paintComponent(Graphics g) { Graphics2D g2 = (Graphics2D) g; g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); AffineTransform af = new AffineTransform(); double[] flatmatrix = new double[6]; af.getMatrix(flatmatrix); printMatrix(flatmatrix); System.out.println(); af.setTransform(1.0d, 0.0d, 0.0d, 1.0d, 10.0d, 20.0d); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.red); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); System.out.println(); af.scale(0.8d, 0.5d); af.getMatrix(flatmatrix); printMatrix(flatmatrix); g2.setTransform(af); g2.setColor(Color.blue); g2.draw(new Rectangle2D.Double(60, 20, 60, 40)); } public static void printMatrix(double[] flatmatrix){ System.out.print("[ " + flatmatrix[0] + " "); System.out.print(flatmatrix[2] + " "); System.out.println(flatmatrix[4] + " ]"); System.out.print("[ " + flatmatrix[1] + " "); System.out.print(flatmatrix[3] + " "); System.out.println(flatmatrix[5] + " ]"); } }実行結果は下記のようになります。
[ 1.0 0.0 0.0 ] [ 0.0 1.0 0.0 ] [ 1.0 0.0 10.0 ] [ 0.0 1.0 20.0 ] [ 0.8 0.0 10.0 ] [ 0.0 0.5 20.0 ]
- リリースノート
[ 目次 ]- 2024/10/14 Ver=2.04 JDK_23 で確認
- 2023/04/23 Ver=2.03 JDK_20 で確認
- 2021/12/03 Ver=1.04 JDK_17 で確認
- 2021/08/07 Ver=1.03 JDK_16 で確認
- 2020/10/23 Ver=1.02 JDK_15 で確認
- 2016/12/15 Ver=1.01 初版リリース
- 関連ページ
[ 目次 ]